Passo-a-passo para um projeto de análise de dados do começo ao fim (incluindo machine learning)

Hermann Vargens
20 de mai. de 2022
10 min de leitura

Atualizado: 1 de set. de 2022

O objetivo deste post é mostrar alguns passos básicos de um projeto de Análise de Dados, onde utilizaremos a técnica de Machine Learning para obter um modelo de predição do preço de um automóvel. Neste artigo, partiremos desde a aquisição dos dados, faremos algum tratamento nos dados, onde vamos selecionar as variáveis mais relevantes para o modelo de predição do preço, e prosseguiremos até a etapa de modelagem. Com as equações em mãos, poderemos responder perguntas do tipo:

O revendedor está oferecendo um valor justo pela minha troca?
O valor que estou pedindo pelo meu carro é justo?

O notebook pode ser encontrado neste link.

1. Aquisição de Dados

1.1 Leitura de Dados

Essa é uma das etapas mais simples de realizar (embora nem sempre) com o uso da biblioteca Pandas. Nosso dataset se encontra no endereço

https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-DA0101EN-SkillsNetwork/labs/Data%20files/auto.csv

Após baixar o arquivo para o computador, vamos importar as bibliotecas necessárias para a manipulação inicial dos dados:

import pandas as pd
import numpy as np

Precisamos criar um DataFrame a partir dos dados. Para isso, usamos a função 'read_csv()', pois o arquivo que baixamos é do tipo CSV. Outros tipos de arquivos como .xls, podem ser transformados em DataFrame também, utilizando outros métodos, como o 'read_excel()'. O argumento do método é o caminho do arquivo.

df = pd.read_csv('.../auto.csv')
df.head()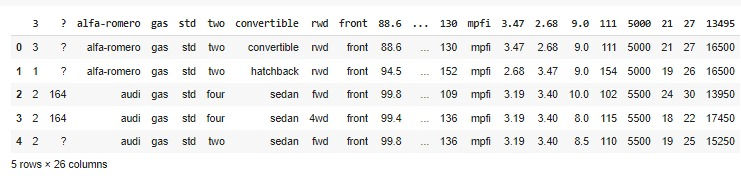

1.2 Cabeçalho

Agora que fizemos o download dos nossos dados e os transformamos em um DataFrame, vamos dar uma olhada mais de perto no cabeçalho:

df.columns

Podemos ver que ele está um tanto bagunçado. Como já sei de antemão a que cada coluna se refere (mas na prática, não é tão fácil assim, dependendo de como a empresa organiza os dados), vamos corrigir isso:

headers = ["symboling", "normalized-losses", "make", "fuel-type", "aspiration", "num-of-doors","body-style", 
         "drive-wheels", "engine-location", "wheel-base", "length", "width", "height", "curb-weight", "engine-type",
         "num-of-cylinders", "engine-size", "fuel-system", "bore", "stroke", "compression-ratio", "horsepower",
         "peak-rpm", "city-mpg", "highway-mpg", "price"]
         
df.columns = headers

Vamos conferir como ficou nosso DataFrame:

df.head()

2. Data wrangling

Também é conhecida por 'manipulaçãoo dos dados', 'pré-processamento dos dados', 'disputa de dados' (não gosto muito dessa), dentre outras denominações. Esta é provavelmente uma das etapas mais longas e trabalhosas, a depender do dataset. Aqui, os dados serão pré-processados, lidaremos com valores ausentes, corrigiremos o formato dos dados, faremos a padronização, "binning", transformaremos variáveis categóricas em numéricas, dentre outras coisas. Vejamos abaixo como executar cada uma dessas partes citadas.

2.1 Valores ausentes

Às vezes, os dados podem vir de uma dataset não muito bem trabalhado, e conter valores como '?', valores nulos, ou ainda espaços em branco. A primeira coisa que temos que fazer é:

Identificar valores ausentes

Vimos que há vários valores com um '?', que não contém dados nenhum. Vamos substituí-los por "np.NaN" (not a number) do pacote Numpy. Isso permitirá que façamos a contagem correta dos valores ausentes, usando o método 'isnull()', seguido de 'sum()'.

df = df.replace('?',np.NaN)

df.isnull().sum()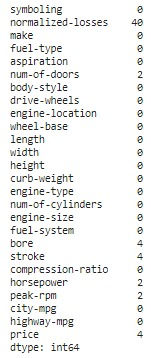

Agora que temos conhecimento da quantidade de dados nulos, precisamos decidir o que fazer com eles.

Lidando com valores ausentes

Aqui temos apenas duas escolhas: excluir as linhas ou colunas que apresentam valores ausentes, ou substituí-los pela média, mediana ou outra função. Cada caso é um caso. Essa é uma das coisas que torna essa etapa tão trabalhosa. Vamos criar uma função que substitua os valores ausentes em "normalized-losses", "stroke", "bore", "horsepower", "peak-rpm", pela média.

Primeiro criamos uma lista chamada de colunas, e que contém os índices das colunas de interesse:

colunas = [1,18,19,21,22]

Ao chamar a função abaixo, os valores de i serão lidos a partir da lista 'colunas', que converterá seu tipo para float, calculará a média, e fará a substituição dos valores ausentes.

def missing_value(i):
  for i in colunas:
    df[df.columns[i]].replace(np.nan, df[df.columns[i]].astype("float").mean(), inplace = True)

Para a coluna "num-of-doors", faremos a substituição usando a frequencia. O valor que aparece mais vezes é 'four' (veremos adiante como calcular isso).

df["num-of-doors"].replace(np.nan, "four", inplace=True)

Finalmente podemos apenas "dropar" (excluir) as linhas da coluna "price", que possui 4 valores ausentes.

df=df.dropna(columns=["price"], axis=0)

Como excluímos algumas linhas, precisamos também reiniciar o índice do dataframe.

df.reset_index(drop=True, inplace=True)

Se conferirmos agora, encontraremos que a quantidade de valores nulos em cada coluna é zero.

df.isnull().sum()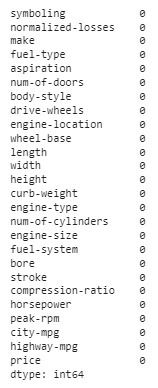

Observação: Assim como transformamos o conjunto de dados (dataset) em um DataFrame, podemos usar o Pandas para fazer o inverso e salvar o novo dataset no computador ou na nuvem: df.to_csv("automobile.csv")

2.2 Corrigir o formato dos dados (dtypes)

Aqui vemos mais a fundo com qual tipo de dado estamos lidando, se são numéricos, representando valores financeiros ou parâmetros de um equipamento, ou se são categóricos como tipo de casa, gênero, grau de instrução, datas, ou ainda se são do tipo 'verdadeiro' ou 'falso', etc. Isso já nos garante alguns insights iniciais. Os cinco principais tipos de dados no Pandas: object, int, float, bool, datetime64. Para fazer uma verificação inicial sobre o tipo de dado em cada coluna, usamos o seguinte método:

df.dtypes

Quando percebemos que algum dado não possui o tipo adequado, podemos corrigi-lo usando o método 'astype()'.

df[["bore", "stroke"]] = df[["bore", "stroke"]].astype("float")
df[["normalized-losses"]] = df[["normalized-losses"]].astype("int")
df[["price"]] = df[["price"]].astype("float")
df[["peak-rpm"]] = df[["peak-rpm"]].astype("float")
df[["horsepower"]] = df[["horsepower"]].astype("float")

Vamos conferir o resultado:

df.dtypes

3. Análise Exploratória de Dados

Após toda a manipulação e transformação que fizemos nos dados, podemos iniciar sua exploração para obter alguns insights iniciais.

3.1 Descrição estatística básica dos dados (describe())

Usamos o método describe() para obter descrições básicas sobre cada coluna (também chamada de feature). São elas: contagem, média, desvio-padrão, valor mínimo, 1º, 2º e 3º quartil e valor máximo. Quando colocamos o parâmetro "include='all' " no argumento, também podemos visualizar alguns dados sobre as variáveis categóricas, como a quantidade de valores únicos, o primeiro e o último valor.

df.describe(include='all')

3.2 Variáveis categóricas

São as variáveis que representam as características dos dados, e seus valores não são numéricos. Como exemplos comuns, temos gênero (M ou F), cor (azul, amarelo, etc), estilo (moderno, contemporâneo, etc) e outros. São exemplos de variáveis categóricas representadas por números (mas não são numéricos), quando tempo, por exemplo tipo 1, 2, 3, etc., grau 1, 2, 3, etc., dependendo da característica de cada dataset. O que caracteriza que esses valores numéricos são variáveis categóricas é que o tipo 2, por exemplo, não é maior ou melhor que o tipo 1, o tipo 3 não é maior ou melhor que o tipo 2, etc.

3.2.1 Distribuição dos valores

Quando queremos ter uma visão geral de como os valores de uma variável se distribuem de acordo com cada grupo, em relação a outra variável, comumente usamos visualizações do tipo 'boxplot' (diagrama de caixa). Sucintamente, o diagrama possibilita verificar rapidamente onde estão localizados 50% dos valores mais prováveis, a mediana e os valores extremos, e assim podemos analisar comos os preços estão distribuidos para cada categoria.

Vamos plotar um gráfico do tipo 'boxplot', tendo no eixo x a coluna 'body-style' e no eixo y a coluna 'price'. Utilizaremos a biblioteca plotly.

import plotly.express as px

fig = px.box(df, x='body-style',y='price')
fig.update_xaxes(title_font=dict(size=24),tickfont=dict(size=18))
fig.update_yaxes(title_font=dict(size=24),tickfont=dict(size=18))
fig.update_layout(title_text="Boxplot do 'body-style'",title_font=dict(size=24))
fig.show()

Podemos ver que praticamente todas as categorias de 'body-style' cobrem uma boa parte da faixa de preços, que significa, na prática, que esta feature pode não contribuir significativamente para a predição dos preços.

Vamos analisar agora as variáveis "engine-location" e "price":

fig = px.box(df, x='engine-location',y='price')
fig.update_xaxes(title_font=dict(size=24),tickfont=dict(size=18))
fig.update_yaxes(title_font=dict(size=24),tickfont=dict(size=18))
fig.update_layout(title_text="Boxplot do 'engine-location'",title_font=dict(size=24))
fig.show()

Diferentemente da situação anterior, vemos que cada tipo de 'engine-location' sobre claramente uma faixa distinta de preços, indicando que esta variável pode ser uma ótima preditora dos preços.

Vamos avaliar também as features "drive-wheels" e "price":

fig = px.box(df, x='drive-wheels',y='price')
fig.update_xaxes(title_font=dict(size=24),tickfont=dict(size=18))
fig.update_yaxes(title_font=dict(size=24),tickfont=dict(size=18))
fig.update_layout(title_text="Boxplot do 'drive-wheels'",title_font=dict(size=24))
fig.show()

Mais uma vez, vemos que as faixas de preços diferem bastante para cada tipo em 'drive-wheels', o que faz dessa variável uma boa candidata para a modelagem. Vamos plotar um boxplot para todas as variáveis categóricas:

from plotly.subplots import make_subplots
import plotly.graph_objects as go

fig = make_subplots(rows=2, cols=5,subplot_titles=("Make vs. Price","Fuel-type vs. Price", "Aspiration vs. Price", "Num-of-doors vs. Price",
                                                   "Engine-tye vs. Price", "Num-of-cylinders vs. Price","Fuel-system vs. Price","Body-style vs. Price",
                                                   "Engine-location vs. Price","Drive-wheels vs. Price"))

fig.add_trace(go.Box(x=df['make'], y=df['price']),row=1, col=1)
fig.add_trace(go.Box(x=df['fuel-type'], y=df['price']),row=1, col=2)
fig.add_trace(go.Box(x=df['aspiration'], y=df['price']),row=1, col=3)
fig.add_trace(go.Box(x=df['num-of-doors'], y=df['price']),row=1, col=4)
fig.add_trace(go.Box(x=df['engine-type'], y=df['price']),row=1, col=5)
fig.add_trace(go.Box(x=df['num-of-cylinders'], y=df['price']),row=2, col=1)
fig.add_trace(go.Box(x=df['fuel-system'], y=df['price']),row=2, col=2)
fig.add_trace(go.Box(x=df['body-style'], y=df['price']),row=2, col=3)
fig.add_trace(go.Box(x=df['engine-location'], y=df['price']),row=2, col=4)
fig.add_trace(go.Box(x=df['drive-wheels'], y=df['price']),row=2, col=5)

fig.update_layout(height=600, width=1300, title_text="Boxplot das variáveis categóricas",title_font=dict(size=24), showlegend=False)

fig.show()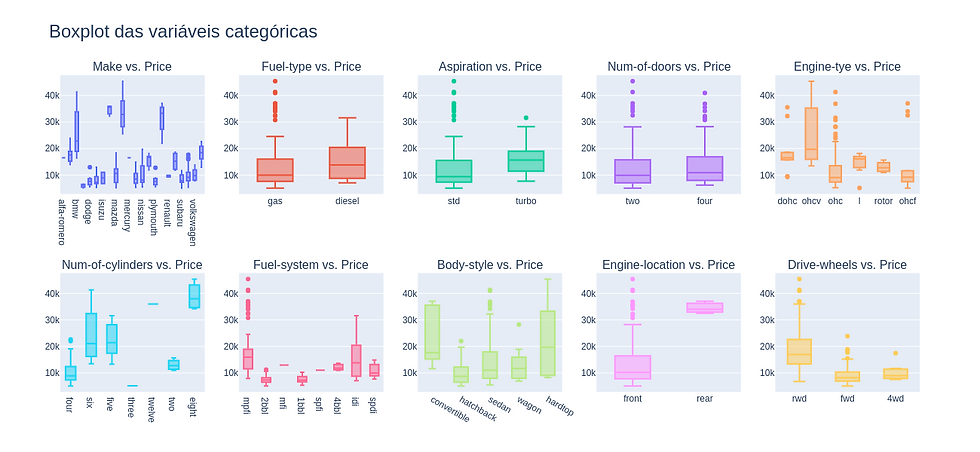

Como podemos ver acima, apenas as variáveis 'engine-location' e 'drive-wheels' apresentam posuem uma distribuição dos preços diferentes para cada grupo dentro da variável, e portanto, elas serão utilizadas para a modelagem.

3.3 Variáveis numéricas

Esse tipo de variável (int ou float) possui valores numéricos. Os exemplos são diversos, medidas de altura, peso, velocidade, tempo, etc.

3.3.1 Correlação

A correlação mede a relação estatística entre duas variáveis contínuas. Em outras palavras, ela mostra o quanto uma variável depende da outra. Existem diversos tipos de coeficientes de correlação, mas a que vamos utilizar aqui, e que está no método 'corr()' é a correlação de Pearson.

O coeficiente de correlação de Pearson mede a relação linear entre duas variáveis contínuas e pode assumir valores entre -1 e 1, sendo que 0 significa ausência de correlação, -1 significa uma correlação negativa (quanto mais uma cresce, mais a outra diminui, e vice-versa) ou positiva (quanto mais uma cresce, mais a outra cresce e vice-versa).

df.corr()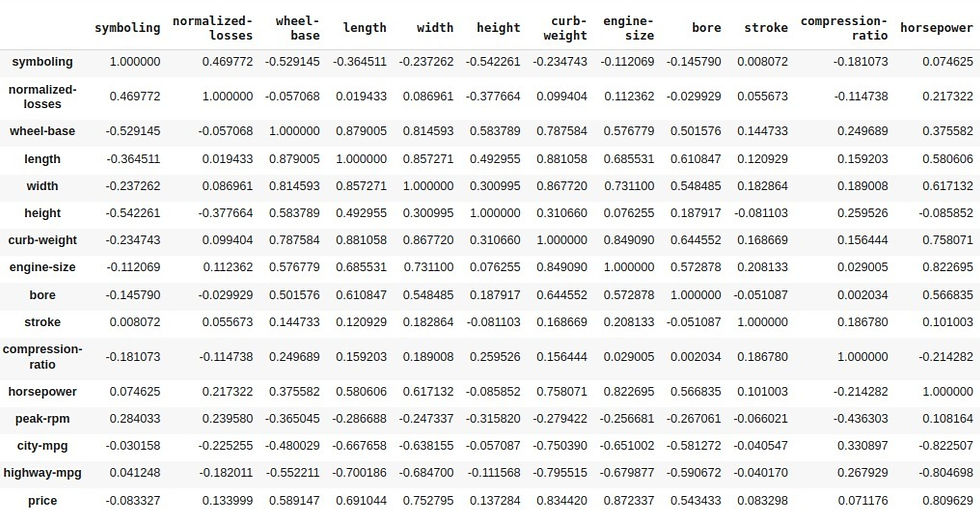

Como queremos verificar a correlação entre cada variável contínua e a variável 'price', vamos extrair apenas a coluna 'price' do DataFrame acima, e orderná-la.

df.corr()[['price']].sort_values(by='price')

Agora podemos ver mais facilmente que as variáveis 'highway-mpg', 'city-mpg', 'bore', 'wheel-base', 'length', 'width', 'horse-power', 'curb-weight' e 'engine-size' são as variáveis que possuem maior influência na variável 'price' (linearmente).

3.3.2 Valor p

Precisamos, então, testar quão estatisticamente significativa é cada correlação. Para isso, usamos o 'valor p'. Por convenção, temos que:

valor p < 0,001: dizemos que há fortes evidências de que a correlação é significativa.

valor p < 0,05: há evidência moderada de que a correlação é significativa.

valor p < 0,1: há fraca evidência de que a correlação é significativa.

valor p > 0,1: não há evidência de que a correlação seja significativa.

Vamos calcular os coeficientes de correlação de Pearson novamente, juntamente com o valor p, para cada coluna numérica. Automatizamos nossa análise, criando um laço para que seja analisada se cada coluna é do tipo numérica, e em caso positivo, deverá ser calculada a correlação de Pearson e valor P. Os dados serão exibidos num dataframe.

from scipy import stats

correlacao_valorP = []
for i in df.columns:
    if df[i].dtypes == 'float64' or df[i].dtypes == 'int64':
        correlacao_valorP.append([i, 
              stats.pearsonr(df[i], df['price'])[0],
              stats.pearsonr(df[i], df['price'])[1]
              ])
              
pd.DataFrame(correlacao_valorP)

onde a coluna 0 representa a variável, coluna 1 representa o coeficiente de correlação de Pearson e a coluna 2 representa o valor p.

Obviamente a correlação entre a coluna 'price' e ela mesma é 1. Todos os valores P são bem próximos de 0, indicando que as correlações estatísticas são significantes. Só nos resta agora selecionar as features com maiores valores de correlação de Pearson para o nosso modelo. São elas:

Length
Width
Curb-weight
Engine-size
Horsepower
City-mpg
Highway-mpg
Wheel-base
Bore

4. Modelagem (Regressão Múltipla Linear)

Como temos várias features, o modelo que vamos utilizar é o de Regressão Linear Múltipla. De forma geral, ele é concebido como:

Y = ax1 + bx2 + cx3 + ...

onde a, b, c,... são os coeficientes da equação, e x1, x2, x3,... representam cada variável.

A primeira etapa para nossa modelagem, será criar um novo DataFrame contendo somente as colunas independentes, ou seja, as variáveis que possuem influência sobre a variável de interesse (target), 'price'.

X = df[['length', 'width', 'curb-weight', 'engine-size', 'horsepower', 'city-mpg', 'highway-mpg', 'wheel-base', 'bore', 'drive-wheels']]

y = df[['price']]

4.1 Transformar variáveis categóricas em numéricas

Quando passamos a etapa de modelagem dos dados, muitos algoritmos não conseguem processar variáveis categóricas. Assim, é importante transformar essas variáveis em valores numéricos. Há algumas formas de se fazer isso, e talvez a mais simples é usar a função 'get_dummies()' do Pandas. Ela cria novas colunas no DataFrame, fazendo com que valores categóricos, como 'Sim', 'Não', assuma valores numéricos como 0 e 1.

X = pd.get_dummies(X,columns=['drive-wheels'], drop_first = True)

(A rigor, o tratamento das variáveis categóricas ficaria para após a divisão entre dados de treino e testes, mas por se tratar apenas de uma conversão de variáveis categóricas para numéricas, não há problemas.)

4.2 Split (divisão dos dados entre treino e teste)

Esta etapa consiste na divisão dos dados emm dois grupos: treino e teste. O dataset de treino deverá 'aprender' como os dados se comportam. É a partir dele que podemos extrair as equações que nos serão úteis. Uma vez treinado o nosso modelo, podemos então utilizá-lo para prever os resultados e comparar com os resultados contidos nos dados de teste. Podemos fazer isso facilmente, utilizando o pacote scikitlearn.

from sklearn.model_selection import train_test_split

x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=1)

Temos então, 4 datasets, sendo 2 de treino, para X e y, e 2 de teste, para X e y.

4.3 Ajuste dos dados

Agora que nossos dados já estão no formato que desejamos, podemos finalmente passar a etapa de ajuste. A primeira coisa que temos que fazer é importar o pacote LinearRegresssion() do sklearn:

from sklearn import linear_model

Em seguida, instanciamos o objeto o qual vamos manipular para fazer o ajuste:

regr = linear_model.LinearRegression()

Agora podemos executar o ajuste e conferir os coeficientes da equação e o ponto de intercecção:

regr.fit (x_train, y_train)

#visualizando os coeficientes e ponto de intersecção obtidos:

print(pd.DataFrame(regr.coef_, columns=X. columns, index=['Coeficientes']).T, '\n')
print ('Ponto de interceção: ', regr.intercept_)

4.4 Avaliação do ajuste (explained variance)

Vamos utilizar como métrica de avaliação do ajuste, o "Explained variance regression score", cuja fórmula é:

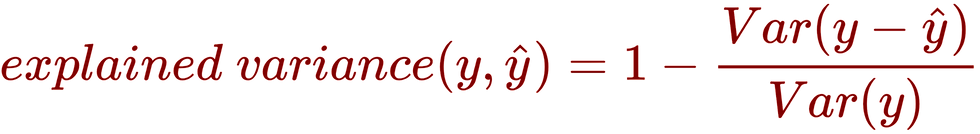
Essa métrica apresenta como resultado valores entre 0 e 1, onde quanto mais próximo de 1, melhor ajusta está o modelo, e melhor sua capacidade de predição, e quanto mais próximo de 0, pior o ajuste. Para os dados de teste, temos:

regr.score(x_train, y_train)

Output:
0.8501800219892778

O valor de 0,8501 está bem próximo de 1 e indica que nosso modelo foi bem sucedido ao ajustar os dados. Vamos checar agora como nosso modelo se comporta com outro conjunto de dados:

regr.score(x_test, y_test)

Output:
0.7724303889257939

Como vemos, há uma queda na performance do modelo, indo a 0,7724. Embora haja um decréscimo, nosso modelo ainda é capaz de fazer boas previsões.

4.5 Avaliação do ajuste (RMSE e MAE)

Outra forma de avaliar se o modelo foi bem sucedido é através das métricas RMSE e MAE. O RMSE (root mean squared error) é a medida que calcula "a raiz quadrática média" dos erros entre valores observados (reais) e predições (hipóteses), enquanto que MAE (mean absolut error) calcula o "erro absoluto médio" dos erros entre valores observados (reais) e predições (hipóteses).

from sklearn.metrics import mean_squared_error
print('RMSE treino:', mean_squared_error(y_train, y_pred_train,squared=False))
print('RMSE teste:', mean_squared_error(y_test, y_pred_test,squared=False))

Output:
RMSE treino: 2976.817374814677 
RMSE teste: 4023.4064399578315

from sklearn.metrics import mean_absolute_error
print('MAE treino:', mean_squared_error(y_train, y_pred_train,squared=False))
print('MAE teste:',mean_squared_error(y_test, y_pred_test,squared=False))

MAE treino: 2976.817374814677 
MAE teste: 4023.4064399578315

4.6 Avaliação por meio de visualização

A última avliação que iremos fazer é a visual. Infelizmente, numa regressão múltipla linear, não conseguimos plotar um gráfico de resíduos. No entanto, podemos utilizar um gráfico de distribuição, comparando a distribuição dos valores ajustados com a distribuição dos valores reais.

import seaborn as sns

sns.distplot(y, hist=False, color="b", label="Valores reais")
sns.distplot(y_pred, hist=False, color="r", label="Valores preditos")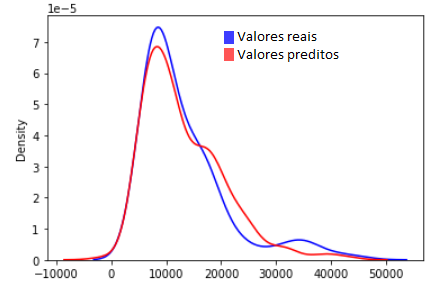

Como podemos verificar na figura acima, nosso modelo de regressão múltipla linear explica bem as variações de preço dentro de certos limites, como até 10000, e apresenta certo erro acima desse valor, especialmente entre 20000 e 30000, e ao redor de 40000.

5. Conclusão

Neste artigo, procurei mostrar a análise de um dataset contendo diversas features e os preços de carros. O objetivo foi mostrar o básico de como fazemos a aquisição dos dados, a transformação em um DataFrame possível de ser manipulado, o trabalho de fazer a limpeza dos dados. Mostramos também como trabalhar com variáveis categóricas e numéricas, ajustando o tipo de dado, transformando variáveis categóricas em numéricas, e trabalhamos na escolha das variáveis mais relevantes para o modelo, através da correlação de Pearson e valor p, onde também obtivemos algumas informações estatísticas, como auxílio de gráficos. Finalmente na última etapa, realizamos o split e a normalização dos dados e a modelagem usando o scikit-learn, e o modelo de Regressão Múltipla Linear.